Writing a Recursive Function

For this challenge question, we are going to get more practice starting with a standard function definition and redefining it as a recursive python function.

This is exactly what we did in the virtual lesson!

Standard Function Definition

The function we will be defining recursively is:

f(n, k) = n × k, with recursion on n ≥ 0.

This is how the standard function will look as a Python function:

    def f(n: int, k: int) -> int:
        return n * k

Recursive Definition

We want to convert it into a recursive function that looks something like this:

    def f(n: int, k: int) -> int:
        if n == 0: #base case
            # <Put something here>
        else: # recursive rule
            # <Put something here>

You can do this by following the steps we took in class.

Looking at the standard function definition, fill in the sequence:

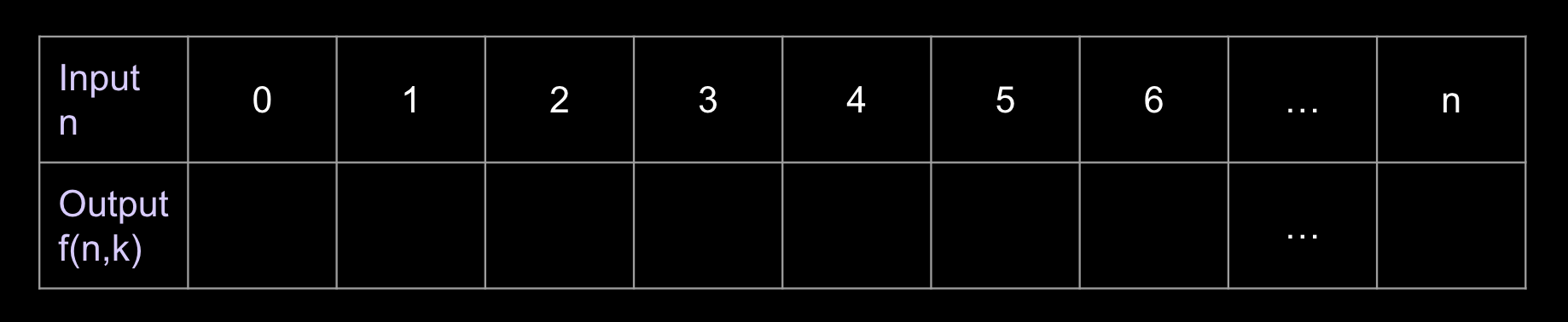
You can find the recursive rule by observing how you get from one output to another.

For example, if I want to know the pattern for getting from f(n − 1, k) to f(n, k), I could ask “How do I get from f(2, k) to f(3, k)? How do I get from f(3, k) to f(4, k)?” and so on. These are just the values in the bottom row, so see if you can find the pattern!

This will help you find out your recursive definition and you can use that to write your function!

Writing the Function

Inside your lessons folder, create a file called recursion.py. Use that file to define f.

Your function should result in the following functionality:

>>> from lessons.recursion import f
>>> f(2,2)
4
>>> f(3,4)
12
>>> f(5,4)
20

Submission

Create a submission by running:

python -m tools.submission lessons/recursion.py